An Open Source Tool for Teaching Analytical Calculations in Engineering Education
Abstract
A core role of an engineer is to predict the performance of a system based on first principles. These predictions can be made using analytical calculations based on the principles of physics and engineering or using numerical simulation tools such as FEA or CFD software. Engineering education tends to emphasize analytical calculations to facilitate a firm understanding of engineering fundamentals. This approach provides a solid base for students as they begin using more advanced numerical simulation approaches later in their engineering education and in industry. This grounding is important since numerical simulation tools tend to shelter users from the details of the physics used and can be easily misused without sufficient understanding of the principles involved. While numerical simulation tools have evolved significantly in their capabilities and ease of use in recent years, the approach to analytical calculations has remained largely unchanged since the days of Euler. As an effort to modernize engineering calculations, the open source engineering software EngineeringPaper.xyz has been developed that runs on any device and provides an easy way to create, document, and share engineering calculations. This paper covers the development and the educational application of EngineeringPaper.xyz.
Introduction
The advent of advanced numerical simulation tools in engineering such as finite element analysis (FEA) and computation fluid dynamics (CFD) has led to great advancements in engineering design by allowing for the design of complex systems such as fuel-efficient aircraft and automobiles with increasing standards of crash safety. Even though these new simulation tools allow for the analysis of more complex geometry than is possible using analytical calculations alone, the simulation tools themselves rely on the same physical principles as the analytical calculations. Therefore, a solid understanding of the analytical approach to solve these problems makes a practicing engineer a more capable user of the more advanced simulation tools. This benefit manifests itself in multiple ways.
The first benefit of analytical solution approaches is that knowing how to perform analytical calculations allows an engineer to check that a simulation is setup correctly and outputting realistic results. Simulations will often give convincing results in situations where the boundary conditions or material properties are wildly inaccurate. Additionally, when setting up complex simulations that involve nonlinear materials or other nonlinear phenomenon, it’s often simpler to run a simple test case where there are analytical solutions available to ensure the simulation boundary conditions and material properties are setup properly before moving on to more complex geometry. This approach gives the engineer confidence that the results obtained from the simulation can be trusted.
The second benefit of analytical solution approaches is that they provide the engineer insight into the relationship between critical parameters involved in a design. For example, consider the equation for the max deflection for a cantilever loaded with a point load at its end:
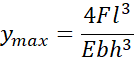
Observing this equation shows that beam deflection has a cubic dependence on both length, l, and cross-sectional height, h, whereas there is a linear dependance on both cross-sectional width, b, and material elastic modulus, E. Note that this knowledge is applicable in any situation where bending stiffness is important, not just in the simple cantilever beam case. Knowledge of these general relationships gives an engineer instant insight into which parameters will have the biggest impact on performance. This insight speeds up the process of homing in on a performant design, which is particularly important for complex simulations that may take many hours, or even days, to complete.
There are many approaches for actual performing analytical calculations including pencil and paper, spreadsheets, and numerical orientated programming languages such as MATLAB or Python. While the pencil and paper approach has the advantage of readability and ease of documentation through explanatory text and illustrations, it has the disadvantage that any changes in parameters requires a partial or complete redo of the calculation. Spreadsheets make it easier to update parameters and have the results automatically update. Spreadsheets also have some advantage in familiarity where most engineers are able to work with a spreadsheet obtained from a colleague without any special instruction. A downside of spreadsheets is that the equation format can be unintuitive and difficult to read for complex calculations. Often, users of spreadsheets created by others view the spreadsheet as a black box. Another approach to analytical calculations is to program the calculation using either the MATLAB or Python programing language. Programming the calculation gives the most flexibility allowing the solving of systems that cannot be solved without implementing a numerical solution technique such as time integration for differential equations. The downside of the programming approach is the difficulty in sharing these calculations with other engineers. It is required that any engineer that runs the program-based calculation to have MATLAB or Python installed and they need to know how to run the program. Additionally, the programming-based approach makes the calculation even more of a black box than the spreadsheet approach since engineers with enough proficiency in MATLAB or Python to be able to fully understand someone else’s code are the exception. The final approach to is to use a specialized engineering calculation package, where Mathcad is the canonical example. Mathcad has the advantage of allowing equations to be entered in natural mathematical notation making the equations intuitive to enter and easy to visually understand. Mathcad also automatically checks for unit consistency throughout the calculation, which helps catch many types of errors. The main drawbacks of Mathcad are its significant cost and that it only runs on Windows PC’s. Also, the only way to share a Mathcad calculation is for both parties to have compatible versions of Mathcad installed on their computers.
The importance of analytical calculations in engineering design and the limitations of the current analytical tools outlined above drove the motivation to develop EngineeringPaper.xyz. Like Mathcad, EngineeringPaper.xyz is a tool dedicated to analytical calculations that uses natural math notation and that automatically tracks and checks units throughout the calculation. EngineeringPaper.xyz is a web-based application that runs in the user’s web browser. Being a web application, EngineeringPaper.xyz runs on any platform including Windows, macOS, Linux, iOS, ChromeOS, and Android. Additionally, the calculations created using EngineeringPaper.xyz can be saved as a shareable link so that anyone can open, use, and edit the calculation without the need to install anything. Finally, that fact that EngineeringPaper.xyz is open source software makes it freely available to anyone, eliminating the financial barrier to adoption.
Software Architecture
Many technologies and open source libraries come together to make EngineeringPaper.xyz possible. The primary enabler is the Pyodide project (Droettboom et al., 2021), which is a WebAssembly port of the entire Python interpreter that allows Python programs to be run in the user’s web browser. WebAssembly is a technology supported by all modern web browsers that allows code to be compiled to target the web browser as an execution target. Because of this, WebAssembly allows software that is not written in JavaScript to run in the browser. The power of Python for engineering calculations comes from its wide array of libraries. Common libraries used for engineering calculations are Numpy for numerical computation (Harris et al., 2020), SymPy for symbolic math (Meurer et al., 2017), Matplotlib for plotting (Hunter, 2007), and Jupyter for organizing the Python code and plots into a notebook format (Granger & Pérez, 2021). EngineeringPaper.xyz utilizes the SymPy library to handle all the calculations and the dimensional analysis required for unit tracking.
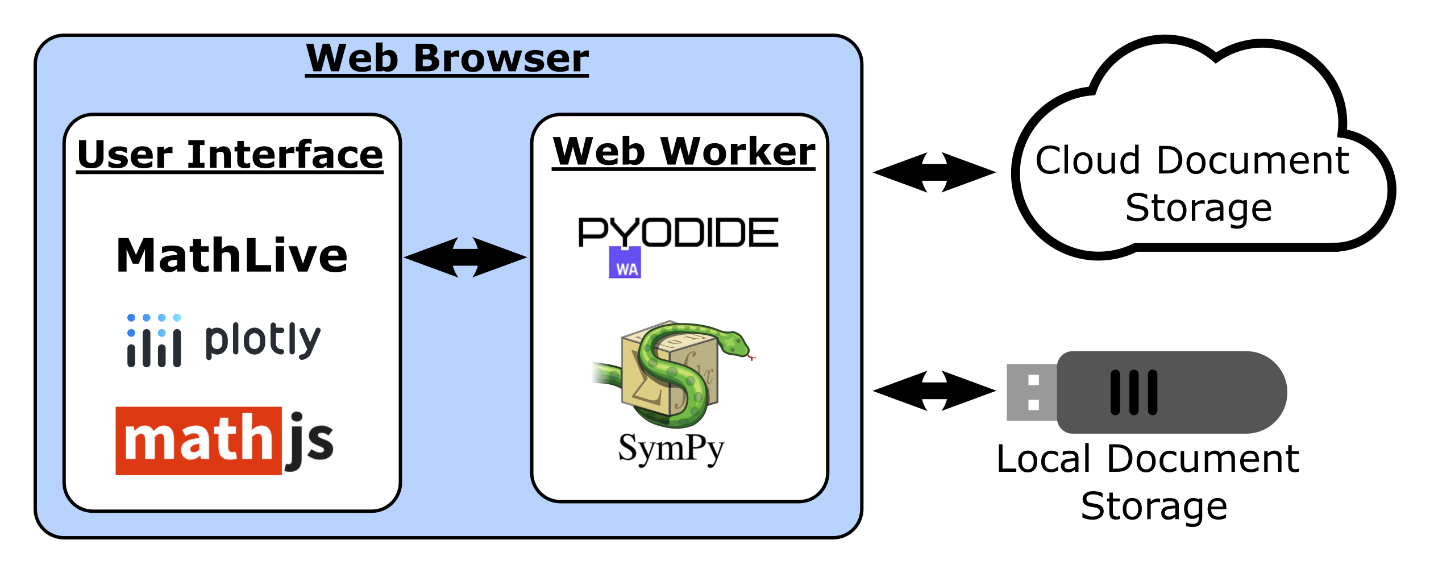
The software architecture for EngineeringPaper.xyz is outlined in Figure 1. All of the calculations run locally on the user’s browser using Pyodide to run the SymPy symbolic math library. The user interface is implemented in TypeScript and runs on the main browser thread. The calculations are run inside a web worker. A web worker provides an execution context outside the main user interface thread of the web page, which allows long calculations to be performed using SymPy without blocking the user interface. For the user interface, the MathLive project is used to provide interactive math expression editing (Gourdol, 2017/2023), Plotly is used for plotting functions (Inc, 2015), and Math.js is used for unit conversions (Jong, 2013/2023).
The math expressions that users input into the MathLive fields are represented in LaTex math markup. These LaTex expressions are converted into SymPy notation using an parser generated using the Antlr4 (Parr, 2013) parser generator. Additionally, all numerical values are converted to the SI unit system for internal calculations. This data is then passed to the web worker as JSON data. The required expression substitutions, dimensional analysis, and numerical evaluation of the mathematical expressions are then performed using Python code that heavily utilizes the SymPy library. Finally, the results are passed back to the user interface in JSON form to be rendered for the user.
There are two approaches that can be used to share documents with others. The simplest way to share a document is to create a shareable link, which stores the document in a cloud storage database. This allows users to send a link to anyone who is then able to access the calculation directly just by clicking a link. A second approach to document sharing is to save a calculation locally as a file. This file can be shared with others who can open the file using EngineeringPaper.xyz. In both cases, the document is serialized into JSON format.
The full source code for EngineeringPaper.xyz is available on its GitHub page (Greminger, 2020/2023) and is released under the MIT open source license.
Features
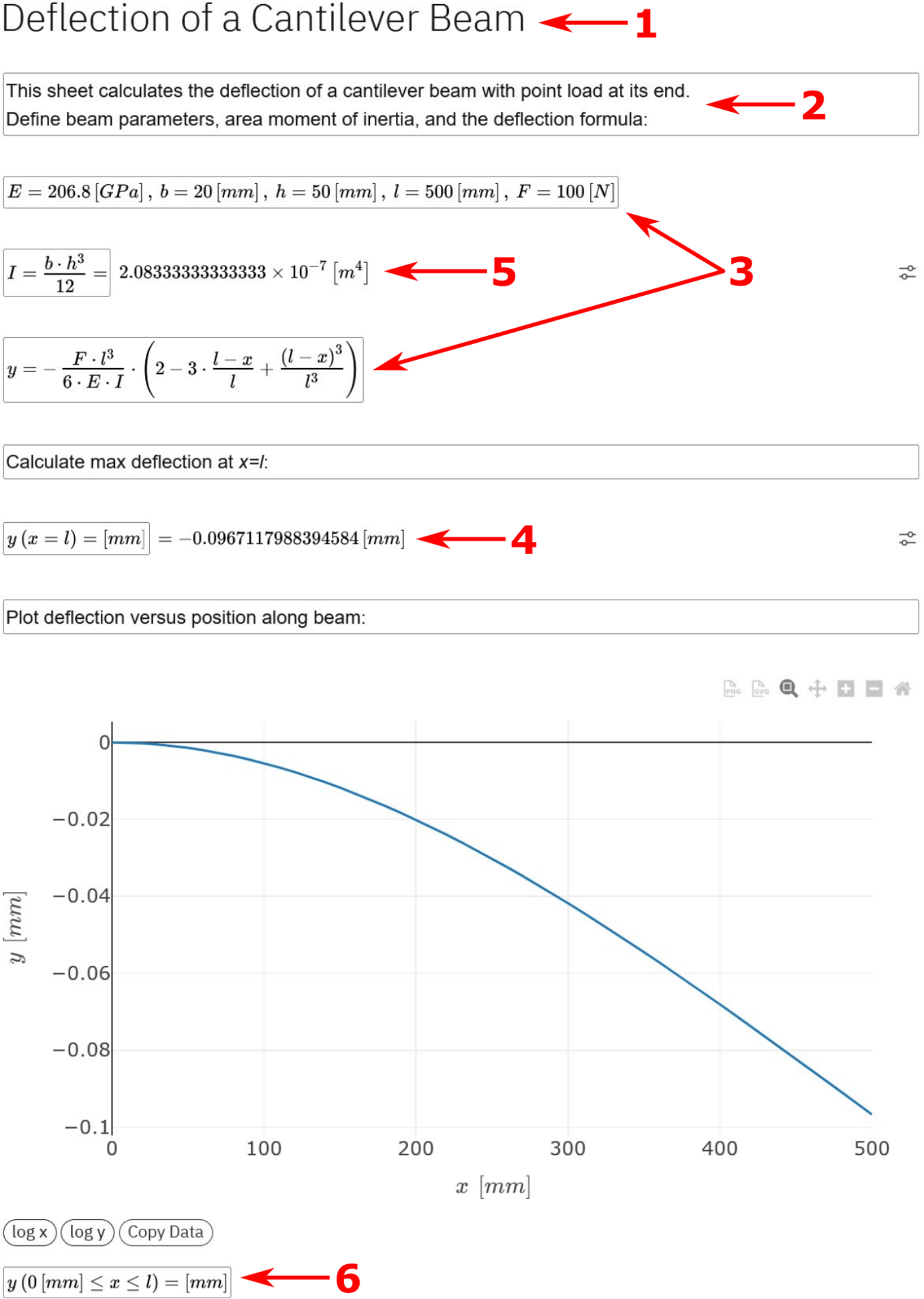
An example EngineeringPaper.xyz document is shown in Figure 2 (the parenthetical numbers in this section refer to the labels in Figure 2). Each document has its own title (1) and can have documentation cells (2) to help document the calculation. The documentation cells can hold both text and images. There are two primary types of math cells in EngineeringPaper.xyz. The first are assignment cells (3) where variables can be defined by placing a variable name on the left-hand side of an equals sign and a mathematical expression on the right hand side of an equals sign. Multiple assignments can be placed in the same cell by separating them with commas. The second type of math cell is a query cell (4) where a mathematical expression is followed by an equals sign. Assignment and query cell types can also be combined into a single cell by appending an equals sign to end of an assignment (5). Units are assigned to numerical values by enclosing the units in square brackets following the numerical value (3). Query statements will always provide answers in SI units (5). Users can specify a custom unit for the results of a query statement by placing units in square brackets following the equals sign (4). If the units for the calculation are not compatible, an error will be indicated.
Variables are automatically treated as functions if all of their parameters are not defined by assignment cells in the document. For example, the definition of y in the example sheet (4) includes the undefined parameter x. Because of this, the parameter x can be passed to y as a function argument in order to call y as a function (4). This function notation can also be used to provide a range of values for the input to create a plot (6), which is a special type of query cell.

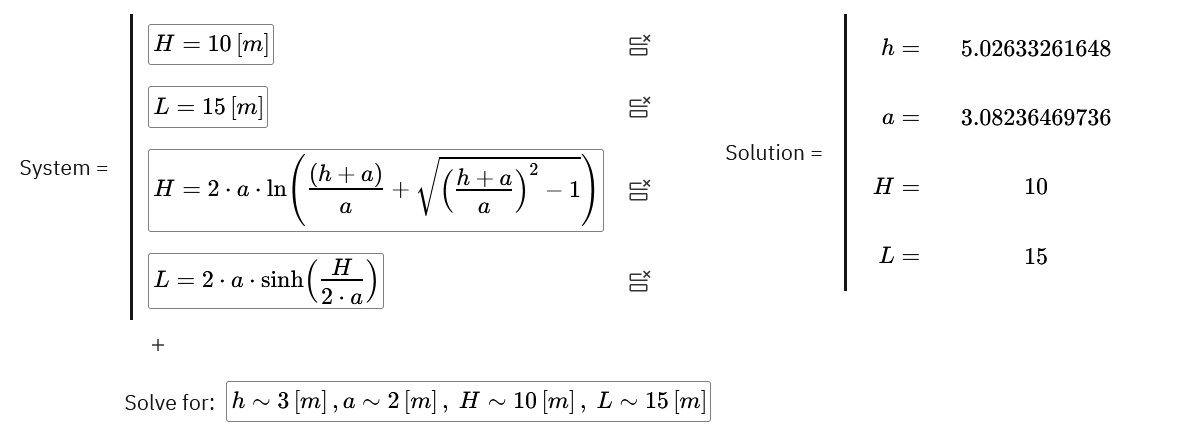
Systems of equations can be solved either exactly or numerically using a system solve cell. Figure 3 shows a system of equations solved exactly. The solutions are treated as assignments and can be used later in the document. For cases where an exact solution is unavailable, a numerical solution can be obtained by providing initial guesses for the parameters to be solved for (see Figure 4).
Piecewise functions often occur in engineering calculations. A piecewise cell type can be used to define a piecewise function as show in Figure 5. For a piecewise expression, the first expression where the if condition is true is assigned to the left hand side parameter. If none of the if conditions are true, the otherwise expression is used.
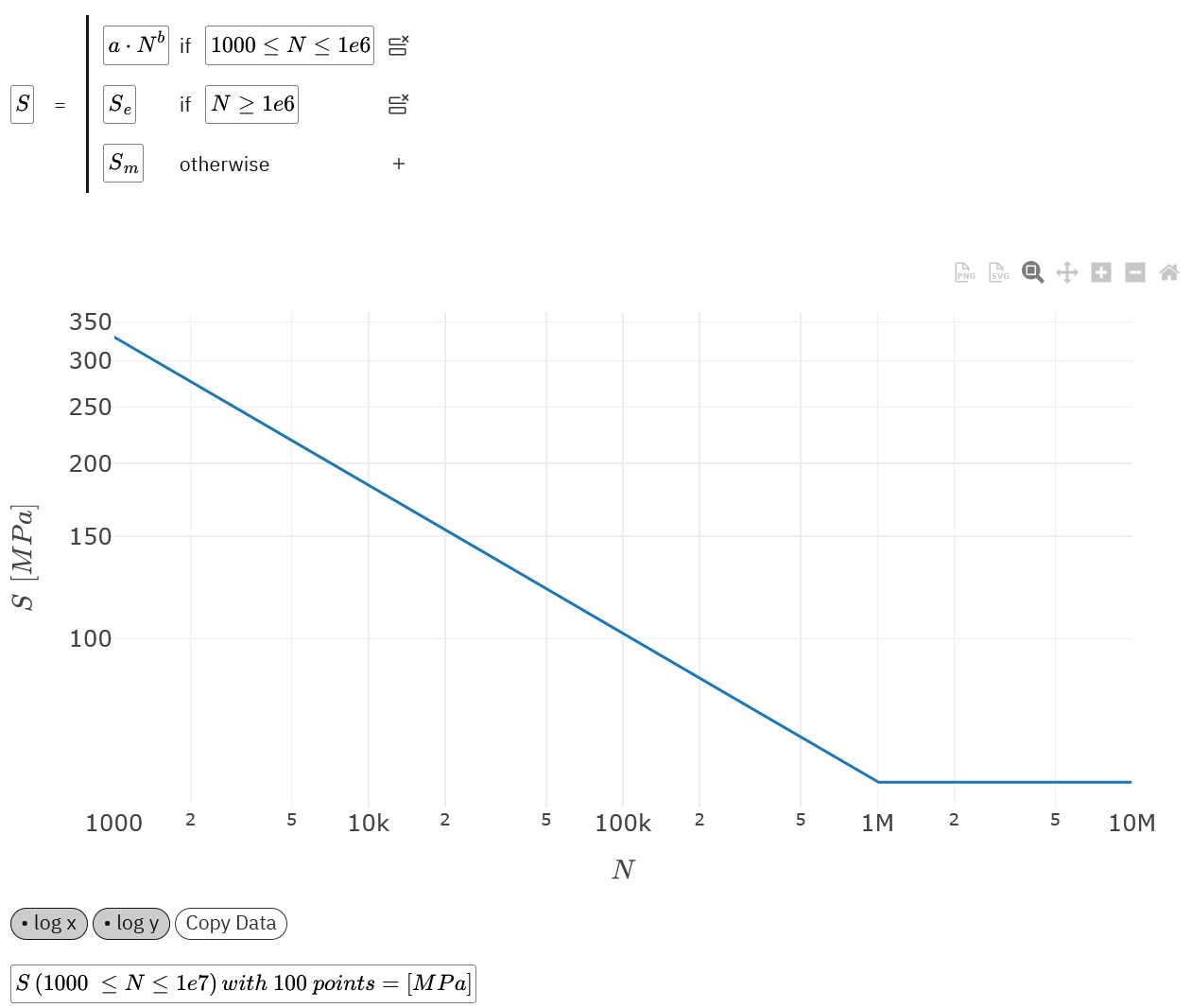
Figure 5: Piecewise function definition at the top and corresponding plot at the bottom.
Application in Engineering Education
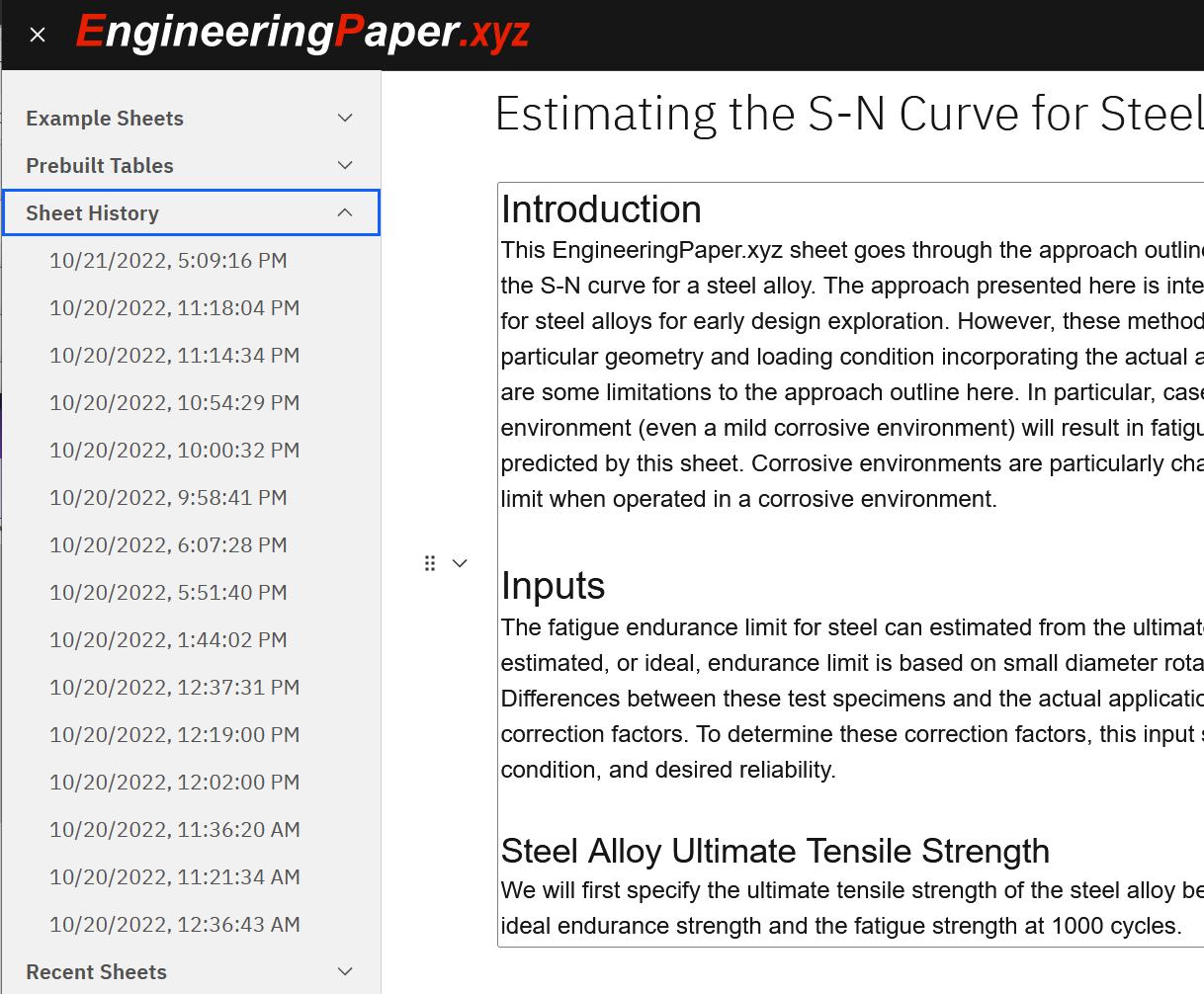
The ease of sharing calculations by creating shareable links makes it possible to share example calculations with students through a course’s learning management system (LMS). It also allows students to easily submit calculations as assignments through the LMS. One issue with having students submit an assignment as a link is the risk of having students submit another student’s work. To minimize this risk, students should be encouraged to place their name in the title or in a documentation cell at the top of their document. Each time a shareable link is created, an entry is placed in the sheet history (see Figure 6). This history can be checked to ensure a student is not submitted a document that was previously submitted by another student.
Conclusions
A new open source tool for engineering calculations has been presented that provides a way to create shareable engineering calculations in natural math notation with automatic unit checking and unit conversion capabilities. In a world where advanced numerical tools allow more complex systems than ever to be simulated, a fundamental understanding of first principals is more important than ever since these tools make it easy to generate results that are meaningless if not checked against fundamentals. However, our current options for engineering calculations are either outdated (paper and pencil), are effectively black boxes when shared (spreadsheets, MATLAB, or Python programs), or are not accessible without significant cost to whoever you need to share the document with (Mathcad). EngineeringPaper.xyz provides a means to create, document, and share calculations that can be opened by anyone with just a link.
EngineeringPaper.xyz is full featured today with the ability to perform a wide variety of engineering calculations. Example calculations are available that cover a range of engineering disciplines (The Official EngineeringPaper.Xyz Blog, 2021). Future features planned to be added include support for vectors and matrices, support for thermodynamic properties such as steam properties, optimization support, and Python code generation.
References
Droettboom, M., Yurchak, R., Chatham, H., Chua, D., Abramowitz, M., casatir, Stafford, J., Tandon, M., Lachance, W., Meyer, J. M., Greminger, M., Trevino, C., Marshall, J., Seering, A., Ollinger, N., Staněk, O., Sergio, Brooks, T. L., Ouyang, W., … chigozienri. (2021). Pyodide/pyodide: [Computer software]. Zenodo. https://doi.org/10.5281/zenodo.5156931
EngineeringPaper-xyz (Director). (2023, June 7). EngineeringPaper.xyz Quick Tutorial (New and Updated!). https://www.youtube.com/watch?v=r7EZQVhcr5Q
Gourdol, A. (2023). A Web Component for Math Input [TypeScript]. https://github.com/arnog/mathlive (Original work published 2017)
Granger, B. E., & Pérez, F. (2021). Jupyter: Thinking and Storytelling With Code and Data. Computing in Science & Engineering, 23(2), 7–14. https://doi.org/10.1109/MCSE.2021.3059263
Greminger, M. (2023). Mgreminger/EngineeringPaper.xyz [TypeScript]. https://github.com/mgreminger/EngineeringPaper.xyz (Original work published 2020)
Harris, C. R., Millman, K. J., Walt, S. J. van der, Gommers, R., Virtanen, P., Cournapeau, D., Wieser, E., Taylor, J., Berg, S., Smith, N. J., Kern, R., Picus, M., Hoyer, S., Kerkwijk, M. H. van, Brett, M., Haldane, A., Río, J. F. del, Wiebe, M., Peterson, P., … Oliphant, T. E. (2020). Array programming with NumPy. Nature, 585(7825), 357–362. https://doi.org/10.1038/s41586-020-2649-2
Hunter, J. D. (2007). Matplotlib: A 2D graphics environment. Computing in Science & Engineering, 9(3), 90–95. https://doi.org/10.1109/MCSE.2007.55
Inc, P. T. (2015). Collaborative data science. Plotly Technologies Inc. https://plot.ly
Jong, J. de. (2023). Josdejong/mathjs [JavaScript]. https://github.com/josdejong/mathjs (Original work published 2013)
Meurer, A., Smith, C. P., Paprocki, M., Čertík, O., Kirpichev, S. B., Rocklin, M., Kumar, Am., Ivanov, S., Moore, J. K., Singh, S., Rathnayake, T., Vig, S., Granger, B. E., Muller, R. P., Bonazzi, F., Gupta, H., Vats, S., Johansson, F., Pedregosa, F., … Scopatz, A. (2017). SymPy: Symbolic computing in Python. PeerJ Computer Science, 3, e103. https://doi.org/10.7717/peerj-cs.103
Parr, T. (2013). The Definitive ANTLR 4 Reference (Second edition). Pragmatic Bookshelf.
The Official EngineeringPaper.xyz Blog. (2021, October 14). The Official EngineeringPaper.Xyz Blog. https://blog.engineeringpaper.xyz/
About the Author
Michael Greminger is an Associate Professor in the Mechanical and Industrial Engineering Department at the University of Minnesota Duluth. He conducts research in the areas of engineering tool development, medical device design, and numerical design optimization and teaches in the areas of mechanical design, CAD/CAM, and finite element analysis. He has six years of industry experience as a design engineer at Seagate Technology and has 10 granted US patents.