Calculating the Natural Frequencies of a Cantilever Beam

The information presented in this blog post is for educational purposes only. It should not be used for engineering design or relied upon as engineering advice.
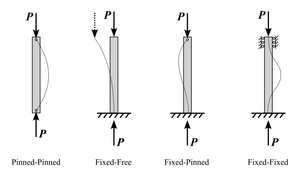
The EngineeringPaper.xyz sheet below (or open in a new tab) shows how to calculate the first 5 natural frequencies and mode shapes for a cantilever beam with a rectangular cross section. The equations used [1] assume that the beam is long and slender. For shorter beams (or for the higher mode numbers of a longer beam) the shear component of the deformation begins to impact the accuracy of the bending mode natural frequencies. See the end of this sheet for a comparison between the analytical solutions and the solutions obtained using finite element simulation (using SolidWorks simulation).
This example also addresses how to correctly handle frequency calculations in EngineeringPaper.xyz that would normally provide results in radians per second. The frequency result needs to be divided by 2π so that it is correctly interpreted has being in Hertz. Without this division by 2π, EngineeringPaper.xyz will incorrectly interpret the frequency units as Hertz since the results will be in [1/sec], even though the correct interpretation without the division by 2π is [rad/sec]. Since EngineeringPaper.xyz will always interpret [1/sec] as being in Hertz, special care always needs to be taken with frequency calculations to explicitly force them to be in Hertz or to be in radians per second. In cases where it is desired to keep the frequency in radians per second, the division by 2π would be removed from the example and the frequency expression would need to be multiplied by 1 [rad] to force EngineeringPaper.xyz to interpret the expression as [rad/sec].
[1] Blevins, Robert D., and R. Plunkett. "Formulas for natural frequency and mode shape." Journal of Applied Mechanics 47.2 (1980): 461.
Calculating the Natural Frequencies of a Cantilever Beam
by u/mgreminger in EngineeringPaperXYZ